코딩테스트 연습 - 미로 탈출
4 1 4 [[1, 2, 1], [3, 2, 1], [2, 4, 1]] [2, 3] 4
programmers.co.kr
문제 설명
신규 게임 ‘카카오 미로 탈출’이 출시되어, 라이언이 베타테스터로 참가했습니다.
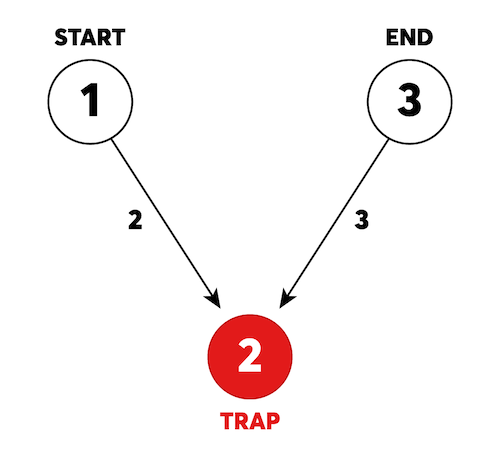
위 예시 그림은 카카오 미로 탈출의 초기 상태를 나타냅니다. 1번부터 3번까지 번호가 붙어있는 3개의 방이 있고, 방과 방 사이를 연결하는 길에는 이동하는데 걸리는 시간이 표시되어 있습니다. 길은 화살표가 가리키는 방향으로만 이동할 수 있습니다. 미로에는 함정이 존재하며, 함정으로 이동하면, 이동한 함정과 연결된 모든 화살표의 방향이 바뀝니다.
출발지점인 1번 방에서 탈출이 가능한 3번 방까지 이동해야 합니다. 탈출하는데 걸리는 최소 시간을 구하려고 합니다.
- 그림의 원은 방을 나타내며 원 안의 숫자는 방 번호를 나타냅니다.
- 방이 n개일 때, 방 번호는 1부터 n까지 사용됩니다.
- 화살표에 표시된 숫자는 방과 방 사이를 이동할 때 걸리는 시간을 나타냅니다.
- 화살표가 가리키고 있는 방향으로만 이동이 가능합니다. 즉, 위 그림에서 2번 방에서 1번 방으로는 이동할 수 없습니다.
- 그림에 표시된 빨간색 방인 2번 방은 함정입니다.
- 함정 방으로 이동하는 순간, 이동한 함정 방과 연결되어있는 모든 길의 방향이 반대가 됩니다.
- 위 그림 1번 방에서 2번 방으로 이동하는 순간 1에서 2로 이동할 수 있던 길은 2에서 1로 이동할 수 있는 길로 바뀌고, 3에서 2로 이동할 수 있던 길은 2에서 3으로 이동할 수 있는 길로 바뀝니다.
- 똑같은 함정 방을 두 번째 방문하게 되면 원래 방향의 길로 돌아옵니다. 즉, 여러 번 방문하여 계속 길의 방향을 반대로 뒤집을 수 있습니다.
- 미로를 탈출하는데 필요한 최단 시간은 다음과 같습니다.
- 1→2: 2번 방으로 이동합니다. 이동 시간은 2입니다.
- 함정 발동: 2번 방과 연결된 모든 길의 방향이 반대가 됩니다.
- 2→3: 3번 방으로 이동합니다. 이동 시간은 3입니다.
- 탈출에 성공했습니다. 총 이동시간은 5입니다.
방의 개수를 나타내는 정수 n, 출발 방의 번호 start, 도착 방의 번호 end, 통로와 이동시간을 나타내는 2차원 정수 배열 roads, 함정 방의 번호를 담은 정수 배열 traps이 매개변수로 주어질 때, 미로를 탈출하는데 필요한 최단 시간을 return 하도록 solution 함수를 완성해주세요.
제한사항
- 2 ≤ n ≤ 1,000
- 1 ≤ start ≤ n
- 1 ≤ end ≤ n
- 1 ≤ roads의 행 길이 ≤ 3,000
- roads의 행은 [P, Q, S]로 이루어져 있습니다.
- P에서 Q로 갈 수 있는 길이 있으며, 길을 따라 이동하는데 S만큼 시간이 걸립니다.
- 1 ≤ P ≤ n
- 1 ≤ Q ≤ n
- P ≠ Q
- 1 ≤ S ≤ 3,000
- 서로 다른 두 방 사이에 직접 연결된 길이 여러 개 존재할 수도 있습니다.
- 0 ≤ traps의 길이 ≤ 10
- 1 ≤ traps의 원소 ≤ n
- 시작 방과 도착 방은 함정이 아닙니다.
- 항상 미로를 탈출할 수 있는 경우만 주어집니다.
입출력 예nstartendroadstrapsresult
| n | start | end | roads | traps | result |
| 3 | 1 | 3 | [[1, 2, 2], [3, 2, 3]] | [2] | 5 |
| 4 | 1 | 4 | [[1, 2, 1], [3, 2, 1], [2, 4, 1]] | [2, 3] | 4 |
입출력 예 설명
입출력 예 #1
문제 예시와 같습니다.
입출력 예 #2
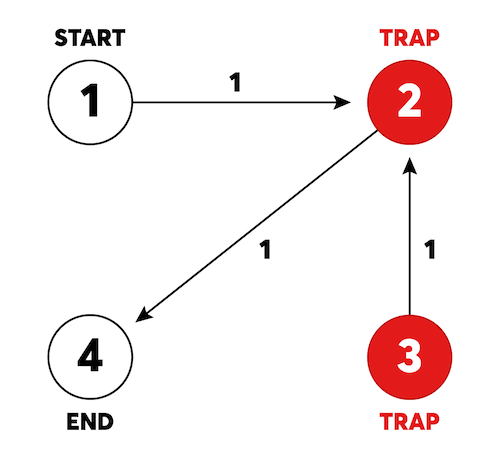
1 → 2 → 3 → 2 → 4 순서로 이동하면 됩니다. 총 이동시간은 4입니다.
풀이
다익스트라와 비트마스크를 물어보는 문제였다고 한다. 다익스트라로 풀어야겠다는 생각을 하지는 못했지만 풀고있는 방식이 사실 다익스트라였다. 다만 trap에 의해 바뀌는 그래프를 계속해서 새로 만들어서 넘겨주다 보니까 5개 정도의 테스트 케이스에서 시간초과 및 실패가 떴다. 불과 얼마 전에 다익스트라와 비트마스크 관련 문제를 풀었던 거 같은데 아는 개념을 제대로 써먹어보지도 못했다는 생각에 현타가 왔다ㅠㅠ
해당 문제는 큰 틀에서는 다익스트라로 start에서 end까지의 최단 경로를 찾아나가지만 trap이라는 제한 조건이 추가된 문제다.
이 영상(https://www.youtube.com/watch?v=1I3hMwQU6GU)의 도움을 많이 받았다.
먼저, 주어진 미로를 표현할 2차원 배열(graph)에 대한 초기값을 지정할 때 주의할 점은 '서로 다른 두 방 사이에 직접 연결된 길이 여러 개 존재할 수도 있다.'는 점이다. 우리는 최단거리를 구할 것이기 때문에 같은 경로의 값이 여러개 나온다면 가장 짧은 것만을 graph에 저장해주면 된다. 또한 자기 자신(graph[i][i])에 대해서는 값을 0을 갖고, roads에서 받은 경로를 제외한 나머지 경로는 길이 없는 것이기 때문에 INF 값을 넣어준다.
int[][] graph = new int[n + 1][n + 1];
Arrays.stream(graph).forEach(x -> Arrays.fill(x, INF));
for (int i = 1; i <= n; i++) {
graph[i][i] = 0;
}
for (int[] road : roads) {
graph[road[0]][road[1]] = Math.min(graph[road[0]][road[1]], road[2]);
}
다음으로는 다익스트라에 대해 이야기해보려고 한다.
이 문제에서는 일반적인 다익스트라 풀이법에 트랩을 고려해야 한다. 트랩의 활성상태 여부를 매 탐색 때마다 업데이트 시키고, 되돌려놓고 하기에는 시간초과가 나기도 하고 문제가 복잡해지기 때문에 비트마스크를 이용한다. 문제 조건에서 최대 트랩의 갯수는 10개로 지정되어 있기 때문에 2^10 정도만에 가능하다.
boolean[][] visited = new boolean[n + 1][1 << traps.length];보통 다익스트라에서 한 정점에서 다른 정점까지의 최단 거리를 1차원 배열로 저장했다면 여기서는 2차원 배열로 저장을 한다.
visited[정점의 번호][트랩 활성 상태]로 표현이 되는데 트랩 활성 상태를 비트마스크로 표현한다. visited는 boolean배열인데 Node에서 최단 거리 비용을 가지고 있기 때문에 visited는 단순히 방문 여부를 체크하기 위해 사용된다.
다익스트라의 탐색 구조는 아래와 같다. 우선순위 큐를 이용하여 Node가 가진 cost가 적은 것부터 나온다.
Queue<Node> queue = new PriorityQueue<>();
queue.add(new Node(start, 0, 0));
while (!queue.isEmpty()) {
Node current = queue.poll();
int state = current.state;
if (current.number == end) { // end에 도달하면 종료
return current.cost;
}
if (visited[current.number][current.state]) { // 방문한 곳이면 넘어감
continue;
}
visited[current.number][current.state] = true;
...
for (int i = 1; i <= n; i++) { // 다음 방문 노드 순회
if (current.number == i) { // 자기 자신은 방문할 수 없음
continue;
}
...
}
}
위 코드에서 ... 부분이 본격적으로 트랩을 지지고 볶는 영역이다. 이제 트랩에 대해 고려해본다.
트랩이 활성화된 경우는 기존의 graph에 저장된 정방향대로 이동하는 것이 아니라 역방향으로 했을 때 이동이 가능한지를 봐야한다.
예를 들어, i에서 j라는 방으로 이동했는데 j가 trap인 경우를 생각해보자. 이동할 때는 graph[i][j]의 가중치를 가지고 이동했을 것이다. 이후 이동때는 trap이 활성화되어 j에서 i로 이동할 수 있게된다. 이때 고려할 가중치는 graph[j][i]가 아닌 graph[i][j]여야 한다. 그래프의 방향이 뒤집어지기 때문이다.
또한 트랩이 활성화 되었다고 해서 graph 자체를 계속해서 바꾸는 것이 아니라 비트마스크로 표현되어있는 트랩의 활성화 여부를 보고 정방향 및 역방향을 고려한다. 역방향 여부를 확인할 때는 현재 노드가 트랩인 경우 뿐만 아니라 다음 노드까지 확인이 필요하다. 현재 노드가 활성화된 트랩이고 다음 트랩도 활성화된 상태라면 역방향의 역방향, 즉 정방향이되기 때문이다.
다음은 넘어온 비트마스크 state를 보고 활성화되어있는 트랩들을 체크하는 로직이다.
boolean currentTrapped = false;
Set<Integer> trapped = new HashSet<>();
for (int i = 0; i < traps.length; i++) {
int bit = 1 << i;
if ((state & bit) != 0) { // 비트에 해당하는 trap이 활성 상태인 경우
if (current.number == traps[i]) { // 그 트랩이 현재 노드인 경우
state &= ~bit; // state에서 이 trap을 비활성화
continue;
}
trapped.add(traps[i]);
continue;
}
// 비트에 해당하는 trap이 활성 상태가 아닌 경우
if (current.number == traps[i]) { // 그 트랩이 현재 노드인 경우
state |= bit; // state에서 이 trap을 활성화
trapped.add(traps[i]);
currentTrapped = true;
}
}currentTrapped는 현재 노드가 활성화된 트랩인지 아닌지 여부를 저장한다. 애초에 트랩이 아닌 경우는 당연히 false다.
trapped는 hashset으로 활성화된 트랩을 저장한다.
for문을 통해서 비트에 해당하는 트랩들이 활성화되어 있는지를 확인해서 trapped에 저장하는 작업인데, 이와 동시에 현재 노드가 트랩인 경우에 상태변경을 해준다. 이미 켜져있는 경우는 state &= ~bit을 통해 꺼주고, 꺼져있는 경우는 state |= bit를 통해 켜준다.
다음은 이후 방문할 노드를 확인하여 우선순위 큐에 넣어주는 작업이다.
for (int i = 1; i <= n; i++) {
if (current.number == i) {
continue;
}
boolean nextTrapped = trapped.contains(i); // 다음 이동할 노드가 trap인지 체크
if (currentTrapped == nextTrapped) { // 현재 노드, 다음 노드 둘다 트랩이거나, 둘 다 아니거나는 결과가 동일
if (graph[current.number][i] != INF) {
queue.add(new Node(i, current.cost + graph[current.number][i], state));
}
continue;
}
// 둘 중 하나가 트랩이라면 그래프의 역방향을 적용
if (graph[i][current.number] != INF) {
queue.add(new Node(i, current.cost + graph[i][current.number], state));
}
}nextTrapped는 다음 노드가 활성화되어 있는 트랩인지를 저장한다. trapped에 해당 방번호가 포함되어 있으면 활성화된 트랩이다.
currentTrapped와 nextTrapped가 같다면, 즉 현재 노드와 다음 노드가 둘 다 활성화된 트랩이거나, 둘 다 활성화되지 않은 트랩(혹은 트랩)인 경우는 정방향 이동을 한다. 그렇지 않으면 역방향을 적용한다.
(코테를 준비하면서 이렇게 알고 있는 개념들을 적용하는 문제를 못풀었을 때가 제일 아쉬운 것 같다. 이 수준까지는 도달해야 실제 테스트에도 유의미한 결과를 낼텐데 말이다. 부족함을 인정하고 더욱더 정진해야겠다고 마음 먹게 해주는 문제였다.)
코드
import java.util.*;
public class Solution {
private static final int INF = Integer.MAX_VALUE;
public int solution(int n, int start, int end, int[][] roads, int[] traps) {
int[][] graph = new int[n + 1][n + 1];
Arrays.stream(graph).forEach(x -> Arrays.fill(x, INF));
for (int i = 1; i <= n; i++) {
graph[i][i] = 0;
}
for (int[] road : roads) {
graph[road[0]][road[1]] = Math.min(graph[road[0]][road[1]], road[2]);
}
// 다익스트라
boolean[][] visited = new boolean[n + 1][1 << traps.length];
Queue<Node> queue = new PriorityQueue<>();
queue.add(new Node(start, 0, 0));
while (!queue.isEmpty()) {
Node current = queue.poll();
int state = current.state;
if (current.number == end) {
return current.cost;
}
if (visited[current.number][current.state]) {
continue;
}
visited[current.number][current.state] = true;
boolean currentTrapped = false;
Set<Integer> trapped = new HashSet<>();
for (int i = 0; i < traps.length; i++) {
int bit = 1 << i;
if ((state & bit) != 0) { // 비트에 해당하는 trap이 활성 상태인 경우
if (current.number == traps[i]) { // 그 트랩이 현재 노드인 경우
state &= ~bit; // state에서 이 trap을 비활성화
continue;
}
trapped.add(traps[i]);
continue;
}
// 비트에 해당하는 trap이 활성 상태가 아닌 경우
if (current.number == traps[i]) { // 그 트랩이 현재 노드인 경우
state |= bit; // state에서 이 trap을 활성화
trapped.add(traps[i]);
currentTrapped = true;
}
}
for (int i = 1; i <= n; i++) {
if (current.number == i) {
continue;
}
boolean nextTrapped = trapped.contains(i); // 다음 이동할 노드가 trap인지 체크
if (currentTrapped == nextTrapped) { // 현재 노드, 다음 노드 둘다 트랩이거나, 둘 다 아니거나는 결과가 동일
if (graph[current.number][i] != INF) {
queue.add(new Node(i, current.cost + graph[current.number][i], state));
}
continue;
}
// 둘 중 하나가 트랩이라면 그래프의 역방향을 적용
if (graph[i][current.number] != INF) {
queue.add(new Node(i, current.cost + graph[i][current.number], state));
}
}
}
return INF;
}
class Node implements Comparable<Node> {
int number;
int cost;
int state;
public Node(int number, int cost, int state) {
this.number = number;
this.cost = cost;
this.state = state;
}
@Override
public int compareTo(Node o) {
return this.cost - o.cost;
}
}
}
'Tech > Problem Solving' 카테고리의 다른 글
| [프로그래머스] 사칙연산 - Java (0) | 2022.02.23 |
|---|---|
| [프로그래머스] 방의 개수 - Java (0) | 2022.02.22 |
| [프로그래머스] 스택/큐 - 다리를 지나는 트럭 (Java) (0) | 2022.02.08 |
| [프로그래머스] Summer/Winter Coding(2019) - 지형 이동 (Java) (0) | 2022.02.07 |
| [프로그래머스] 2021 KAKAO BLIND RECRUITMENT - 합승 택시 요금 (Java) (0) | 2022.02.05 |

