https://www.acmicpc.net/problem/6588
6588번: 골드바흐의 추측
문제 1742년, 독일의 아마추어 수학가 크리스티안 골드바흐는 레온하르트 오일러에게 다음과 같은 추측을 제안하는 편지를 보냈다. 4보다 큰 모든 짝수는 두 홀수 소수의 합으로 나타낼 수 있다. 예를 들어 8은 3 + 5로 나타낼 수 있고, 3과 5는 모두 홀수인 소수이다. 또, 20 = 3 + 17 = 7 + 13, 42 = 5 + 37 = 11 + 31 = 13 + 29 = 19 + 23 이다. 이 추측은 아직도 해결되지 않은 문제이다. 백만 이하의 모
www.acmicpc.net
접근 방식
에라토스테네스의 체 알고리즘을 이용해 소수를 먼저 구해 소수 리스트를 만든다.
입력 값 중 가장 큰 값을 기준으로 그 값보다 작은 소수를 구한다.
매 입력값 때마다 소수 리스트를 구하게 되면 메모리 초과가 발생하니 유의하자.
두 소수를 구해나가는 방법으로 투 포인터 알고리즘을 이용했다.
먼저 가장 작은 소수의 리스트 인덱스(s)와 입력 값(target) 보다 작은 소수 중 가장 큰 수의 인덱스(e)를 구한다.
다음 그림은 target이 8인 경우의 그림이다.
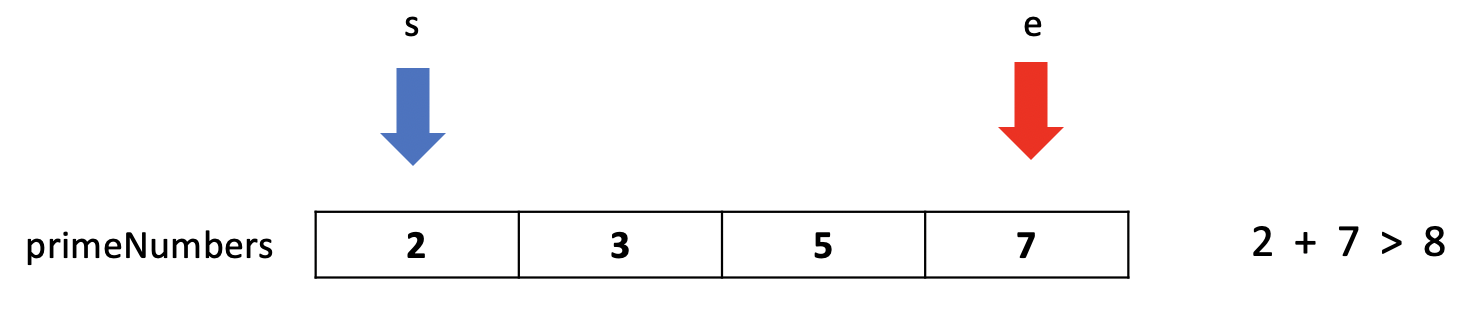
s번째 소수와 e번째 소수를 더하는데, 위 그림과 같이 두 수의 합이 target 보다 큰 경우 e--를 하여 아래와 같이 다시 시도한다.

이번에는 두 수의 합이 target보다 작아졌다. 이러한 경우에는 s++를 하여 다시 시도한다.

시도하면 다음과 같이 target과 같이 동일해 지는 경우가 발생한다.
만약 값이 존재하지 않는다면 s와 e가 리스트 범위를 벗어나게 될 것이다. 그러한 경우에는 문제 조건과 같이 "Goldbach's conjecture is wrong."를 출력하도록 구현했다.
소스 코드
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
private static final String NOT_FOUND_MESSAGE = "Goldbach's conjecture is wrong.";
private static List<Integer> primeNumbers = new ArrayList<>();
private static int max = 0;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
List<Integer> numbers = new ArrayList<>();
int input = scanner.nextInt();
while (input != 0) {
numbers.add(input);
max = Math.max(max, input);
input = scanner.nextInt();
}
setPrimeNumbers(max);
for (int target : numbers) {
int s = 0;
int e = setEndPoint(target);
while (primeNumbers.get(s) + primeNumbers.get(e) != target) {
// 두 소수의 값이 대상보다 작으면 s++, 크면 e--
if (primeNumbers.get(s) + primeNumbers.get(e) < target) {
s++;
} else if (primeNumbers.get(s) + primeNumbers.get(e) > target) {
e--;
}
if (s >= primeNumbers.size() || e < 0) {
System.out.println(NOT_FOUND_MESSAGE);
break;
} else if (primeNumbers.get(s) + primeNumbers.get(e) == target) {
System.out.printf("%d = %d + %d\n", target, primeNumbers.get(s), primeNumbers.get(e));
break;
}
}
}
}
// 인자로 받는 수 보다 작은 소수 중 가장 큰 소수의 리스트 원소를 리턴한다.
private static int setEndPoint(int target) {
int result = 0;
if (target == max) {
return primeNumbers.size() - 1;
}
for (int i = 0; i < primeNumbers.size(); i++) {
if (target < primeNumbers.get(i)) {
result = i - 1;
break;
}
}
return result;
}
// 입력 받은 값 중 가장 큰 수를 기준으로 그 수 이하의 소수를 모두 구해 리스트를 만든다.
private static void setPrimeNumbers(int max) {
boolean[] isNotPrime = new boolean[max + 1];
isNotPrime[0] = true;
isNotPrime[1] = true;
for (int i = 2; i < isNotPrime.length; i++) {
int next = i + i;
if (!isNotPrime[i]) {
while (next <= max) {
isNotPrime[next] = true;
next += i;
}
}
}
for (int i = 2; i < isNotPrime.length; i++) {
if (!isNotPrime[i]) {
primeNumbers.add(i);
}
}
}
}
'Tech > Problem Solving' 카테고리의 다른 글
| [백준 1463] 1로 만들기 (Java) (0) | 2020.02.21 |
|---|---|
| [백준 1003] 피보나치 함수 (Java) (0) | 2020.02.21 |
| [백준 1644] 소수의 연속합 (Java) (0) | 2020.02.14 |
| [백준 2485] 가로수 (Java) (0) | 2020.02.13 |
| [백준 2580] 스도쿠 (Java) (0) | 2020.02.13 |



